Study Guide: Series FLEX Elementary Education Subtest II (918)

Overview

Please note that the sample items featured in this study guide are comprised of 150 to 300-word responses. These sample items and responses are meant to serve as practice materials for the FLEX Elementary Education assessments and do not represent the requested formatting for the FLEX assessments. To meet the requirements of any FLEX assessment, be sure to follow the instructions provided in the Series FLEX Handbook, prompts, and templates. For this FLEX assessment, responses should satisfy Competencies 0002 and 0007.

Competencies:

Recommendation for individuals using a screenreader: please set your punctuation settings to "most."

0002 Understand mathematical reasoning and problem solving, communication and representation, and data analysis.

Descriptive Statements:

Apply knowledge of various strategies and procedures used in problem-solving situations.
Apply knowledge of a variety of diagrams, models, charts, manipulatives, and other tools used to represent mathematical concepts and real-world situations.

0007 Understand the nature of science and the processes of scientific inquiry.

Descriptive Statement:

Apply knowledge of the scientific method, including the design of scientific investigations, systematic observation, and controlled experimentation.

Sample Open-Response Item #1:

Use the information provided in the exhibits to complete the assignment that follows.

Using your knowledge of Earth and space science, as well as your knowledge of representing and interpreting data, analyze the information provided and write a response of approximately 150 to 300 words, or 1 to 2 pages, in which you:

Use proportional reasoning to calculate the approximate height of the tree in feet. Be sure to show the steps you used to arrive at your answer.
Explain how and why the length and direction of the tree's shadow changes between 9:00 a.m., noon, and 6:00 p.m.

Exhibit

Students are measuring the length of their shadows at different times of the day. Students observe that their shadows appear longer in the morning and late afternoon, with the shadows being shortest at noon. The teacher is 72 inches tall. The students measure the teacher's shadow at 3:00 p.m. and record it as 96 inches long. At the same time, a nearby tree casts a shadow that is 19 feet long. The students model the teacher's shadow and the angle of the Sun with the diagram shown below.

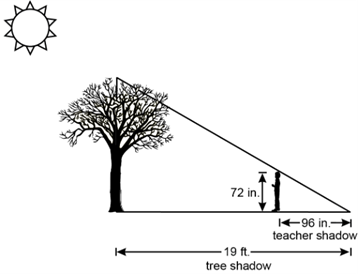
An outdoor scene of a sun, tree, and person are shown. The sun, the top of the tree, and the top of the person's head are positioned along the same line. A line segment that represents the hypotenuse of a right triangle extends from the top of the tree to the top of the person's head and continues until it touches the ground. From the point, another line segment extends left, passing through the bottom of the person's feet to the base of the tree. From that point, another line segment extends upward from the point to the top of the tree, completing the triangle.Three dimensions are provided: the person is 72 inches tall; the horizontal distance from their feet to the right vertex of the triangle, labeled teacher's shadow, is 96 inches; and the distance of the bottom leg of the triangle, labeled tree shadow, is 19 feet.

Sample Strong Response to Open-Response Item #1

Show Sample Strong Response to Open-Response Item #1

The sample response below reflects a strong knowledge and understanding of the subject matter.

The triangle that's formed by the height of the teacher and the length of their shadow is similar to the triangle that's formed by the unknown height of the tree and the length of its shadow. Both triangles have the same ratio of height to base. Changing 72 inches and 96 inches to feet (by dividing each by 12 inches/foot) yields 6 feet and 8 feet. (See computation and Graphic #1 below.)

As the Earth rotates on its axis, the sun appears at different positions in the sky—lower and in the east in the morning as it rises, higher and more overhead at noon, and then lower and in the west at the end of the day as it sets.

The shadow cast by the tree will point in the opposite direction from where the light comes from the sun. At 9 a.m. the shadow will point to the west, at 6 p.m. the shadow will point east. Because the sun is lower at these times, these shadows will be longer than at noon when the sun is more overhead and the shadow cast is short. (See Graphic #2 below.)

72 inches to 96 inches is the same as six feet to 8 feet, and both ratios are equivalent to 3 to 4

So, 6 over 8 equals x over 19

Cross multiply to get:
8 x equals 6 times 19
8 x equals 114
x equals 14 point 2 5

The tree is about 14 point 2 5 feet tall.

14 point 2 5 over 19 equals 3 over 4

This ratio is the same as the teacher and their shadow.

Graphic #1

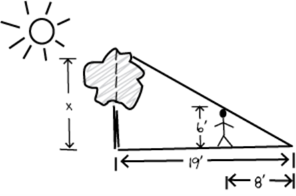
An outdoor scene of a sun, tree, and person are shown in a hand drawn diagram. The sun, the top of the tree, and the top of the person's head are positioned along the same line. A line segment that represents the hypotenuse of a right triangle extends from the top of the tree to the top of the person's head and continues until it touches the ground. From the point, another line segment extends left, passing through the bottom of the person's feet to the base of the tree. From that point, another line segment extends upward from the point to the top of the tree, completing the triangle.In this drawing, the height of the tree is labeled x, the height of the person is labeled 6 feet, the total length of the bottom leg of the triangle is 19 feet, and the distance from the person to the vertex of the triangle that is opposite the tree is 8 feet.

Graphic #2

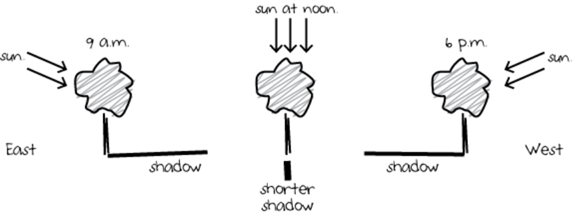
A hand drawn diagram depicts how sunlight and the tree's shadow change for three times during the day.At 9 a m, arrows indicating sunlight are shown pointing at the tree from its eastern-facing side and are angled slightly below horizontal. The shadow is shown extending from the base of the tree toward the direction labeled west.At noon, the arrows for sunlight point directly downward toward the tree. A short vertical line segment is drawn under the tree and it labeled shorter shadow.At 6 p m, arrows indicating sunlight are shown pointing at the tree from on its western-facing side and are angled slightly below horizontal. The shadow is shown extending from the base of the tree toward the direction labeled east.

Sample Open-Response Item #2:

Use the information that appears in the exhibits to complete the assignment that follows.

Using your knowledge of life science, as well as your knowledge of representing and interpreting data, analyze the information provided and write a response of approximately 150 to 300 words, or 1 to 2 pages, in which you:

Calculate and then compare the median heart rate before physical activity and the median heart rate after physical activity. Be sure to show the steps you used to arrive at your answer.
Explain the relationship between the circulatory and respiratory system that results in the changes observed in the table due to physical activity.

Exhibit

Students are investigating the interaction of the human circulatory and respiratory systems. Students work in groups of three: one student acts as the subject, one student measures the subject's breathing rate, and one student measures the subject's heart rate. First, the students measure the breathing and heart rates while the subject is standing at rest. Next, the subject runs in place for 1 minute. Immediately following this physical activity, the students measure and record the subject's heart rate and breathing rate again. Data obtained by 10 student groups for their 10 different subjects are shown in the table below.

intentionally left blank	Before Physical Activity Respiratory Rate (breaths per minute)	Before Physical Activity Heart Rate (beats per minute)	After Physical Activity Respiratory Rate (breaths per minute)	After Physical Activity Heart Rate (beats per minute)
Group 1	28	68	37	128
Group 2	15	72	21	160
Group 3	19	60	35	150
Group 4	17	68	24	140
Group 5	30	70	54	132
Group 6	28	66	48	123
Group 7	32	61	55	115
Group 8	21	56	45	120
Group 9	28	72	40	142
Group 10	25	62	38	130

Sample Strong Responses to Open-Response Item #2

Show First Sample Strong Response to Open-Response Item #2

1. To calculate the median, we list all numbers in the data set from lowest to highest, then find the value that falls in the middle. There are 10 values in each set provided in the Exhibit, so the median falls between the fifth and sixth numbers.

The data for heart rate before physical activity:
56, 60, 61, 62, 66, 68, 68, 70, 72, 72
The fifth and sixth numbers are 66 and 68, so the median is 67 beats per minute.

The data for heart rate after physical activity:
115, 120, 123, 128, 130, 132, 140, 142, 150, 160
The fifth and sixth numbers are 130 and 132, so the median is 131 beats per minute.

We can therefore see that the median heart rate almost doubles after physical activity.

2. To see the relationship between circulatory and respiratory systems, we can find the median respiratory rate for comparison.

Respiratory rate before physical activity:
15, 17, 19, 21, 25, 28, 28, 28, 30, 32
The fifth and sixth values are 25 and 28; we can average these two numbers to find the median: 25+28=53, and 53 divided by 2 equals 26.5 breaths per minute.

Respiratory rate after physical activity:
21, 24, 35, 37, 38, 40, 45, 48, 54, 55
The fifth and sixth values are 38 and 40, so the median is 39 breaths per minute.

Cells require oxygen to perform cellular respiration and as a result, give off carbon dioxide as waste. The more one's muscle cells work during exercise, the more oxygen they need and the more carbon dioxide they give off. This means the heart needs to pump faster to deliver more oxygenated blood to muscle cells, which accounts for the increased heart rate after physical activity. In turn, one's breathing rate also increases to bring more oxygen into the lungs, where the bloodstream picks up oxygen. The carbon dioxide that muscle cells produce as waste also enters the bloodstream, returns to the heart, and is pumped to the lungs for exhalation.

Show Second Sample Strong Response to Open-Response Item #2

To find the median heart rates before and after exercise, list the rates in order from lowest to highest, then find the middle.

56, 60, 61, 62, 66, [the median falls in the middle here - between 66 and 68] 68, 68, 70, 72, 72
The median heart rate before exercise is 67.

115, 120, 123, 128, 130, [the median is between 130 and 132] 132, 140, 142, 150, 160
The median heart rate after exercise is 131.

The median heart rate increased from 67 beats per minute at rest to 131 beats per minute after running in place, demonstrating that exercise causes one's heart to beat faster. The table shows that this holds true for every student measured, and that each student's respiratory rate increased after exercise as well. For example, the student measured in Group 1 saw their respiratory rate increase from 28 to 37 breaths per minute and their heart rate increase from 68 to 128 beats per minute after running. In Group 2, the student's respiratory rate increased from 15 to 21, and their heart rate increased from 72 to 160. This pattern holds for every student measured because the respiratory and circulatory systems work together to provide cells with oxygen. When the student runs, their muscles work harder, their cells use more oxygen, and they breathe faster to keep up with that demand. When they breathe in, red blood cells pick up oxygen from the lungs. Oxygen-rich blood then flows to the heart, which pumps it to the rest of the body. The students' respiratory and heart rates therefore increase to transport oxygen to the muscle cells that need it during exercise. The bloodstream also removes carbon dioxide that cells produce as waste and sends it back to the heart, which then pumps it back to the lungs to be exhaled.

Top of Page