NES Profile: General Science (311)

Dissolving table salt in water elevates the boiling point of the salt solution. This colligative property of the salt solution is most directly affected by which of the following factors?

1. the reactivity of sodium and chloride ions
2. the concentration of the solute dissolved in the solution
3. the specific heat capacity of the solution
4. the reduced hydrogen bonding between water molecules

Correct Response and Explanation (Show Correct ResponseHide Correct Response)

B. This question requires the examinee to analyze the colligative properties of solutions (e.g., freezing point, boiling point, osmotic pressure, vapor pressure). Colligative properties, such as the boiling point and freezing point of a substance, have been shown experimentally to be influenced by the number of particles present in the system, but not the properties of the particles themselves. Therefore, the concentration of salt in the solution is the factor that most directly affects the solution's boiling point.

Calcium chloride (CaCl₂) is a strong electrolyte. If 1.00 mol of CaCl₂ is dissolved in water to make 1.00 L of solution, what is the concentration of chloride (Cl⁻)(Cl negative ) ions in the solution?

1. 0.500 M
2. 1.00 M
3. 1.50 M
4. 2.00 M

Correct Response and Explanation (Show Correct ResponseHide Correct Response)

D. This question requires the examinee to apply knowledge of stoichiometry and the mole concept in balancing chemical equations and solving problems involving the mass relationships of reactants and products. Molarity (M) is the concentration of a solution expressed as moles of solute per liter of solution. The calcium chloride solution has a concentration of 1.00 mol. Each molecule of calcium chloride (CaCl₂) contains two chloride ions. So for every mole of calcium chloride dissolved to make the solution, 2 moles of chloride ions disassociate from each calcium chloride molecule. Therefore, the concentration of chloride ions in solution is 2.00 M left parenthesis start fraction 2.00 mol Cl negative over 1.00 L solution end fraction right parenthesis.

A student performing the calorimetry experiment described above determines that the temperature of the final reaction mixture is 18°C18 degrees Celsius. Which of the following conclusions is supported by the data generated in this experiment?

1. The specific heat of reactant A is greater than that of reactant B.
2. The reaction between reactant A and reactant B is endothermic.
3. The calorimeter has too low of a heat capacity.
4. The reaction between reactant A and reactant B is exothermic.

Correct Response and Explanation (Show Correct ResponseHide Correct Response)

B. This question requires the examinee to demonstrate knowledge of the laws of thermodynamics and the principles of calorimetry, including solving basic calorimetry problems. The change in the temperature of the reaction mixture from 25°C25 degrees Celsius to 18°C18 degrees Celsius indicates that the reaction has absorbed energy from its surroundings. A reaction that absorbs energy from its surroundings is defined as an endothermic process.

An object released from rest slides down a frictionless inclined plane. After 1 s, the object has a speed of 2 m/s and has traveled a distance of 1 m from its starting point, as shown in the diagram below.

The plane is a diagram of a right triangle that is resting on the side opposite the hypotenuse, with the right angle at the bottom left. The object is sliding from left to right down the hypotenuse.

Which of the following tables gives the correct values for the speed of the object and the distance the object has traveled from its starting point at the given times?

1. Time (s)	0	1	2	3	4
   Speed (m/s)	0	2	2	2	2
   Distance (m)	0	1	2	3	4

2. Time (s)	0	1	2	3	4
   Speed (m/s)	0	2	4	6	8
   Distance (m)	0	1	2	3	4

3. Time (s)	0	1	2	3	4
   Speed (m/s)	0	2	4	6	8
   Distance (m)	0	1	4	9	16

4. Time (s)	0	1	2	3	4
   Speed (m/s)	0	2	4	9	16
   Distance (m)	0	1	3	8	15

Correct Response and Explanation (Show Correct ResponseHide Correct Response)

C. This question requires the examinee to analyze motion in terms of concepts of displacement, velocity, and acceleration. Since the inclined plane is frictionless, the object will slide down the plane with constant acceleration due to the component of the gravitational force in the direction of the inclined plane. A characteristic of constant acceleration is that the speed of the particle will increase at a constant rate with respect to time, but the distance the object travels depends on the square of the time elapsed, d =equals 1 half, a times d squared. In response C, the speed at one second intervals is given by 0, 2, 4, 6, 8, which is increasing at a constant rate with respect to time while the distance traveled is given by 0, 1, 4, 9, 16, which depends on the square to the time, t.

Students measure the frequency of the waves generated in a microwave oven using the following procedure. They place a large dish covered with a thin layer of chocolate fudge inside the microwave oven and turn on the oven for about 40 seconds, making certain that the dish does not rotate. When they remove the dish, they observe several melted spots on the fudge, as shown in the diagram below. The students measure the distance, d, between corresponding melted spots and find the average to be about d = 6.0 cmd equals 6.0 cm.

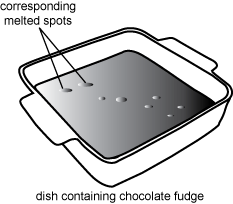
There are bubbles on the surface of the fudge. They appear mostly in pairs in a diagonal line from one side of the pan to the other. One pair is labeled corresponding melted spots.

The students next argue that the distance between the corresponding melted spots represents one-half the wavelength of the microwaves and use the formula c = f λ, with λ = 2d = 12.0 cmc equals f lambda, with lambda equals 2d equals 12.0 cm and c the speed of a microwave, to solve for f, the frequency of the waves.

Which of the following best justifies the assumption that λ = 2dlambda equals 2d?

1. d represents the average value of the microwave amplitudes.
2. d represents the distance between a crest and a trough of a standing wave.
3. d represents the angle of refraction of the microwaves passing through the fudge.
4. d represents the average speed of the waves times the wave period.

Correct Response and Explanation (Show Correct ResponseHide Correct Response)

B. This question requires the examinee to analyze the properties of waves (e.g., speed, frequency, wavelength). A microwave oven generates electromagnetic waves. Electromagnetic waves, like all waves, obey the superposition principle, which states that two or more electromagnetic waves can be combined together to create a resultant wave. The waves may add (if they are in phase) or subtract (if they are out of phase). Microwave ovens are designed so that the electromagnetic waves confined in the space inside the microwave oven reflect off the walls and recombine in such a way as to produce a standing wave (also called a stationary wave). This phenomenon is identical to that of a wave on a plucked string that is fixed at both ends, such as on a guitar string. The diagram below represents the nodes and antinodes of a standing electromagnetic wave. The nodes of a standing wave are where the reflected waves subtract and the wave amplitude is zero. The antinodes are where the reflected waves add together to create a maximum amplitude. At the antinodes, the electric field associated with the wave will transmit the maximum amount of energy to the water molecules in the fudge, causing them to gain molecular motion and increase in temperature, melting the fudge. Therefore, if the melted regions are formed by the antinodes of the standing waves, then they correspond to the crest and trough of a standing wave. As can be seen in the diagram, if L represents the wavelength of the standing wave, then the distance between the melted regions should be one-half of the wavelength, or L = 2dL equals 2d, which justifies the assumption made by the students.

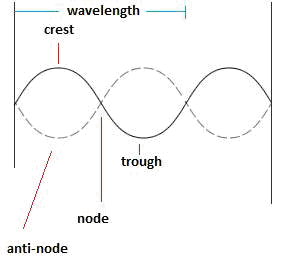
Additional labels identify the high point as the crest and the low point as the trough. An additional wave is shown by a dashed line, offset by half a wavelength. The point where the first wave's crest and additional wave's trough align is labeled anti-node, and the point where the two waves cross is labeled node.

During the late nineteenth century, Thomas Edison developed a direct current system for generating and delivering electricity to homes and businesses. With the ideas of Nikola Tesla, George Westinghouse developed an alternating current system that had many advantages over Edison's direct current system. The advantages of an alternating current system ultimately led to its widespread adoption, and it is the system in use today. A major advantage of the alternating current system over the direct current system was that electricity could be:

1. distributed more efficiently over power lines at very high voltages and then stepped down with a transformer for use in homes and businesses.
2. generated from a single source for use in electrical systems that were wired either in series or in parallel.
3. produced using hydroelectric generators, the dominant source of energy for electric power plants in the nineteenth century.
4. used in homes and businesses safely without having to undergo a step-down in voltage at a transformer station.

Correct Response and Explanation (Show Correct ResponseHide Correct Response)

A. This question requires the examinee to analyze the operation of series and parallel circuits and the relationship between electric current, voltage, and resistance described by Ohm's law. The power transmitted over a conducting wire is given by the product of the current and the voltage. Thus, the same power can be transmitted using either low current and high voltage, or high voltage and low current. The direct current electrical power distribution system developed by Edison used a relatively low voltage and a high current. Because all wires have electrical resistance, wires carrying current dissipate energy as heat. The greater the current in a wire, the more heat the wire will dissipate. Edison's high current system therefore resulted in high energy loss. This meant that power could not be transmitted over long distances and would require many more power plants located near people's homes. Tesla's alternating current system was able to use transformers to transmit power at a high voltage and low current, thereby reducing the heat generated due to the resistance of wire. Power could be transmitted over greater distances with less energy loss. The high voltage could then be converted, or "stepped down" to a fairly low voltage by transformers located near a residence or business.